The gender gap in 100-meter dash times

In 2004, the journal Nature published a short paper by Tatem and colleagues. In that paper, the authors use linear regression to fit curves to Olympic gold medal times for men and women in the 100-meter dash. They note the shrinking gap between men's and women's times, and based on their regression, they predict that in the year 2156 women runners would beat men for the first time.

The authors apply a model selection procedure to a range of regression models, but they are unable to reject the linear model as the best fit to the data. (We admit to being unable to figure out exactly what their model selection procedure was). Knowing some of the authors by reputation, we're convinced that this was a tongue-in-cheek commentary on model selection and the dangers of extrapolation rather than the exceptionally sloppy thinking that would be necessary to think that the linear model is actually a good choice for long-range extrapolation.

Nonetheless, a number of readers rushed to call bullshit on the straight-faced claims that the authors made. To our delight, a high school biology class in College Station, Texas dismantled the original model with considerable flair. But our favorite response is simple, non-technical, and utterly devastating. It's a beautiful model of how one can call bullshit in a way that is persuasive to laypersons and professional statisticians alike. Kenneth Rice uses a type of argument known as reductio ad absurdum, in which one shows that accepting the targeted claim leads to absurd or impossible consequences. He writes:

Sir — A. J. Tatem and colleagues calculate that women may out-sprint men by the middle of the twenty-second century (Nature 431,525; 2004). They omit to mention, however, that (according to their analysis) a far more interesting race should occur in about 2636, when times of less than zero seconds will be recorded.

In the intervening 600 years, the authors may wish to address the obvious challenges raised for both time-keeping and the teaching of basic statistics.

Masterful.

As the Texas high schoolers point out, the problem is that the authors have taken a relatively narrow time range of 104 years and used this extrapolate several hundred years into the future. Moreover, the authors have done so in the absence of any underlying conceptual or mechanistic model of how record performances might change. If one is going extrapolate well beyond the range of the available data, it should done based upon models that account for the known physical processes involved. What should those be? Well, even if we don't have a very good idea of what factors influence 100-meter dash times, we can still do at least something. Namely, there must be some limits to human performance. Even if we are extremely conservative about what these may be, we can be certain that times will not become negative. So a model fit should be constrained to remain positive, reaching an asymptote no lower that zero at the very extreme. Doing so rules out the linear approach taken here.

Since the Nature paper was published, we've had three additional Olympic games. It is interesting to add the results from those three games (yellow and green points below) and see how the model has performed.

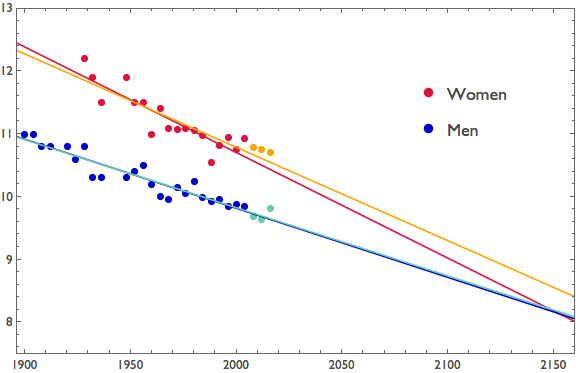
Unsurprisingly, the results from those games all lie within the confidence intervals from the original linear model. Over short time periods, extrapolation seems to be working. However, the model for men performs better than the model for women. After twelve more years, the men's regression line is essentially unchanged, continuing in its downward trajectory by the stellar sub-9.7 times that Usain Bolt recorded in 2008 and 2012. But three recent women's times landed well above the 2004 regression line, and as a result the new regression line that we get when we account for the new data point (orange in the plot) flattens out substantially. It's still steeper than the men's line, meaning that the regression lines still cross, but that crossing now happens eighty-some years after what was predicted using the data through 2004. This in and of itself would offer cause for concern about the original model.

Finally, we figure if you can extrapolate forward into the future you should be able to extrapolate back into the past as well. The first Olympic games were held in 776 BC in Olympia Greece. Our understanding is that the main running race there covered a distance of one stade, or about 190 meters. Had there been a 100 meter event, though, the regression model that Tatem and colleagues have provided predict a winning time of almost exactly 40 seconds — a speed of 2.5 m/sec and the pace of a reasonably brisk walk. While we don't have hard evidence, we have faith that these ancient athletes would have been able to do considerably better.

What conclusions can we draw from this tale of over-extrapolation?

If we follow the inferential lead of Tatem et al., we think we can safely conclude — based on this one article —that all of the statistical analyses published in Nature must be bullshit.